Most models for quantum spin liquids are concerned with spin-1/2 degrees of freedom, but certain types of Mott insulators with orbital degeneracies as well as correlated insulating states in moiré heterostructures (with both spin and valley degrees of freedom) can be described by effective Kugel-Khomskii-type spin-orbital models.

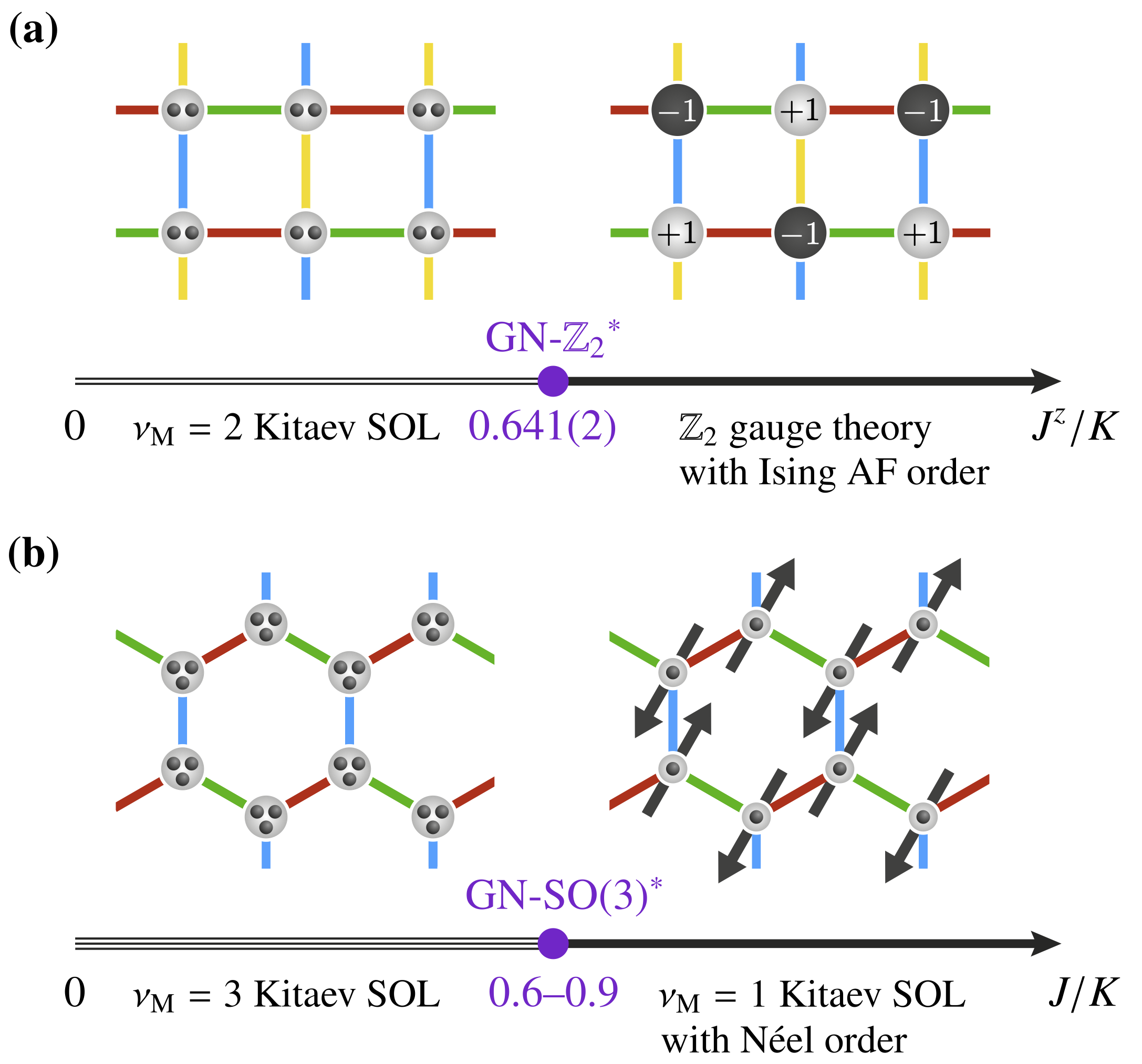
We were able to show that a large family of such models with bond-dependent interactions can be mapped into exactly solvable Z2 lattice gauge theories with multiple flavors of gapless Majorana fermions [1]. This insight allowed us to obtain the first systematic construction of microscopic lattice models for all topological orders classified in Kitaev’s sixteenfold way [2].

We have also discovered that Heisenberg spin-spin interactions in these spin-orbital liquids induce interactions among the Majorana fermions, but keep the Z2 gauge structure intact [3]. At finite coupling, these interactions lead to a phase transition with spontaneous symmetry breaking: the resulting phase features intertwined antiferromagnetic order (spin sector) and topological order (orbital sector). The corresponding fractionalized quantum-critical point lies in a novel SO(N) Gross-Neveu universality class.